Euler Examples

Search

Towers of Hanoi

by Rene Grothmann

This is just a simple recursive solution of the problem of towers of Hanoi. In case you never heard about it, have a look at

http://en.wikipedia.org/wiki/Tower_of_Hanoi

>function move (from:string, to:string, spare:string, n:index) ...
   if n==1 then from|" -> "|to,
   else
     move(from,spare,to,n-1);
     move(from,to,spare,1);
     move(spare,to,from,n-1);
   endif;
 endfunction

Let's go

>move("A","B","C",1)

A -> B

>move("A","B","C",2)

A -> C
A -> B
C -> B

>move("A","B","C",3)

A -> B
A -> C
B -> C
A -> B
C -> A
C -> B
A -> B

>move("A","B","C",4)

A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C
A -> B
C -> B
C -> A
B -> A
C -> B
A -> C
A -> B
C -> B

Animate the Game

Let us try to animate the Towers. I will develop the animation here instead of in an Euler as it should be done.

First we draw a single tower. We use very basic routines for this in plot coordinates x=0...1, y=0...1 and full window mode. The stones are drawn with plotbar.

The discs are stored in a vector, where the discs have positive numbers corresponding to their sze.

>function drawtower (n:index, v:vector, kmax:index) ...
   window([0,0,1024,1024]);
   hold on;
   setplot(0,1,0,1);
   h=0.05; d=0.01; x=n/3-1/6; y=1/2-kmax/2*(h+d); w=1/8; 
   barstyle("0#"); 
   barcolor(red); plotbar(x-w,y,2*w,h);
   barcolor(green);
   for vd=v;
     if vd==0 then break; endif;
     y=y+h+d;
     wd=w*vd/(kmax+1);
     plotbar(x-wd,y,2*wd,h);
   end;
   hold off;
 endfunction

Let us test this.

>clg; drawtower(1,[5,4,3,1,0,0,0],7);

The following function plots three columns stored in a matrix with three rows.

>function drawtowers (v:real, kmax:index) ...
   clg;
   loop 1 to 3
     drawtower(#,v[#],kmax);
   end;
 endfunction

To copy the image to the screen, we use a cropped insimg command.

>v=[5,4,3,1;2;0]; drawtowers(v,7); insimg(crop=[0.3,0.8]);

The next function moves one disc from tower i to tower j. We determine the minimal index k, such that v[i,k] contains a disc.

>function movedisc (v:real, i:index, j:index) ...
   k=max(nonzeros(v[i])); d=v[i,k]; v[i,k]=0;
   if v[j,1]==0 then v[j,1]=d;
   else k=max(nonzeros(v[j])); v[j,k+1]=d;  
   endif;
 endfunction

Let ust test this.

>v=[5,4,3,1;2;0];  ...
   movedisc(v,1,3); drawtowers(v,7); insimg(crop=[0.3,0.8]);

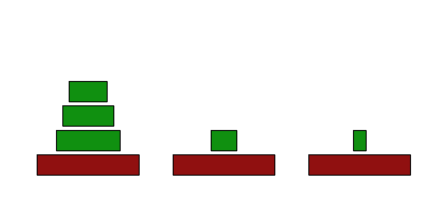
The vector is changed, since matrices are passed by reference, and we change only elements of the matrix.

>shortestformat; v

      5       4       3       0 
      2       0       0       0 
      1       0       0       0 

Now, we move another disc.

>movedisc(v,3,2); drawtowers(v,7); insimg(crop=[0.3,0.8]);

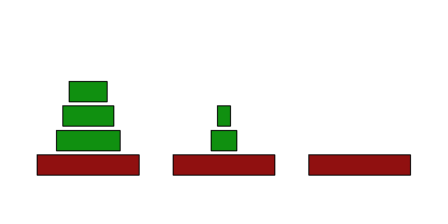
To solve the towers we setup the start position, and call a solve routine, which does the job.

>function solvetowers (n:index=5, delay=0.5) ...
   v=(n:-1:1)_0_0;
   drawtowers(v,n+2); wait(delay);
   solvetowersrec(v,n,n+2,delay);
 endfunction

The solve routine calls a recursive routine as above.

>function solvetowersrec (v,n,kmax,delay) ...
   movetowersrec(v,n,1,2,3,kmax,delay)
 endfunction

This is the recursion.

It moves n-1 discs, then one disc (the largest), then the n-1 discs back.

>function movetowersrec (v,n,from,to,over,kmax,delay) ...
   if n>0 then
     movetowersrec(v,n-1,from,over,to,kmax,delay);
     movedisc(v,from,to); drawtowers(v,kmax); wait(delay);
     movetowersrec(v,n-1,over,to,from,kmax,delay);
   endif;
 endfunction

Start the animation.

>solvetowers(5);

You can set the delay to 5 seconds, and advance by pressing any key. The wait() function is interrupted by key strokes.

>solvetowers(3,delay=5);

Examples